BS808: The Golden Cuboid system for designating volumetric items.
David Noel
<davidn@aoi.com.au>
Ben Franklin Centre for Theoretical Research
PO Box 27, Subiaco, WA 6008, Australia.
Metric paper sizes -- A4 etc
As of 2021, most of the countries of the World, other than a few under strong United States influence, have adopted the international ISO 216 standard as their national standard for paper sizes. These are commonly called Metric Paper Sizes.
Although adoption of this international standard (which was based on the German DIN standard of 1922) took place mostly in the Twentieth Century, its roots are much older, going back to Lichtenberg's proposal of 1786. The basis is to make the ratio of the longer side to the shorter side, of any sheet of paper in the scheme. a fixed ratio. This "Golden Ratio" is equal to the square root of 2 (about 1.4142) [1].
The big advantage of this system is that if any given size of paper is divided parallel to its shorter side into exactly equal halves, each of the new halves has exactly the same proportions of the original. This means that a page of text or an image can be reduced or enlarged to fit on another size of paper in the same series, without any distortion of its proportions.
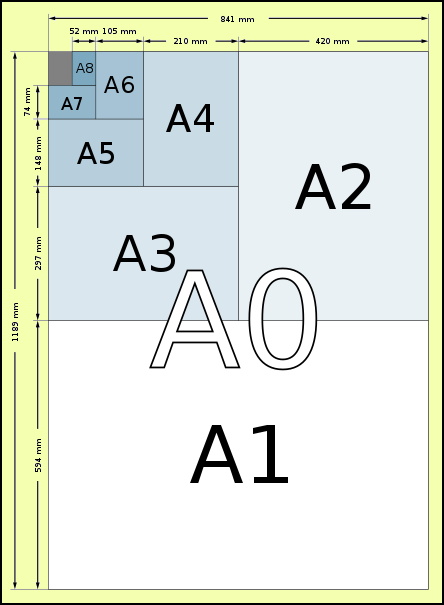
Figure BS808-F1. Metric paper sizes. From [1].
If we call the length of the longer side "a", and that of the shorter side "b", then the area of the sheet is "a" times "b", Area = ab. Adding a second identical sheet next to it makes a combined sheet with sides 2b and a. For the proportions of the two sheets to be exactly the same, then the Golden Ratio R is equal to a/b or 2b/a. A bit of algebra gives you that if (a/b)=(2b/a), a2=2b2. so a2/b2=2, and the Golden Ratio is the square root of 2.
The Metric Paper Size scheme as shown in Figure F1 fixes sheet sizes along a range. The base size, called A0, has an area of exactly 1 square metre. For it to comply with the Golden Ratio, the two sides must have lengths of 1189 and 841 mm (rounded to the nearest whole millimetre), so the surface area of the A0 sheet is 1189 x 841 or 999,949 square millimetres -- just a tiny amount under the theoretical amount of 1,000,000 square millimetres (because of the rounding).
If you live in a developed country which still has broadsheet newspapers, you may find that an opened-out (double-page) broadsheet is A1 in size, and so has an area of half a square metre. Tabloid newspapers may be 1 size down, a double page then is A2, a single page is A3. Standard copying machines are based on A4 paper, those with reduction or enlargement facilities may let you reduce A3 to A4, or go up from A4 up to A3, with the images in exact proportion -- American paper sizes lack this ability.
Golden Cuboids -- scalable volumes
It is possible to develop volume ranges which have the same sort of scalability as metric paper sizes, that is, when cut in half along their waist, the two new shapes will have exactly the same ratios of sides as the original.
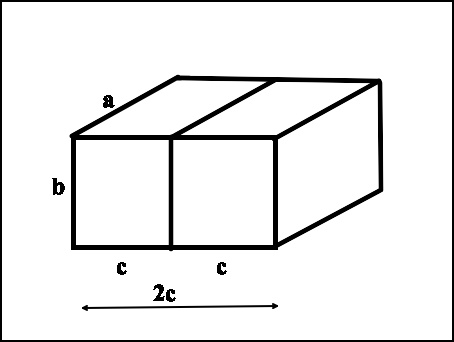
Figure BS808-F2. The Golden Cuboid system of shape volumes.
For illustration look at Figure F2. This depicts two cuboids (rectangular bodies) side by side. The one on the left has a long side "a", an intermediate side "b", and a short side "c". If we wish, we can again use the Golden Ratio (square root of 2, about 1.4142) to fix the relative sizes of the cuboids, giving us Golden Cuboids.
For example, in Figure F2, we fix the ratios of sides so a/b = b/c =2c/a = 1.4142. Cuboids with this ratio have some important properties.
Golden Cuboids are Nestable
The most useful feature of Golden Cuboids is that they are Nestable. This means, that within a given size series, it may be possible to fit 2 or more smaller units in the range, into the single space or part of the single space occupied by a larger unit in the range.
For this to work, an Endpoint must be established for the range, and other sizes in the range worked out from that. Consider the following table (Figure F3) for the "X" Range, based on metric paper sizes.
.jpg)
Figure BS808-F3. The X-Series range of Golden Cuboids.
In this range, the Endpoint was fixed by making the largest face of the first member of the range, called X0, the same as the A0 member of the metric paper range (and hence with an area of 1.0 square metres). This range is in diminishing sizes, and could be extended on to X5, X6, etcetera if these had a practical use.
Another Endpoint could be established based on the first member, called Y0, having a volume of exactly 1.0 cubic metres, and extending the range into increasing sizes (Figure F4).
.jpg)
Figure BS808-F4. The Y-Series range of Golden Cuboids.
Ranges based on other Endpoints are possible, but for Cuboids to be nestable, they must all be in the same Range.
Another possible useful feature in Golden Cuboids is that they may naturally accommodate varying sizes of objects with minimum waste of space. For example, a passenger car will be longer than it is wide, and its width may be less than its height, Natural objects, such as rocks, may also fit better.
* * * * * * * * * * * * * * * * * *

References and Links
[1]. Paper size. https://en.wikipedia.org/wiki/Paper_size .
Go to the Base Sciences Home Page

Version 1.0 compilation started 2021 May 22. First version 1.0 on Web 2021 Jun 4.




.jpg)
.jpg)

