BS809: Graphic Representations of Black Holes and other Vortex Stars
and some Bold Propositions on the Universe
David Noel
<davidn@aoi.com.au>
Ben Franklin Centre for Theoretical Research
PO Box 27, Subiaco, WA 6008, Australia.
Black Holes
Black Holes are a hot topic in cosmology and astrophysics, and various graphic representations of these have been developed over the years. These graphics are useful in visualizing the roles black holes play in the cosmos, but most older versions are no longer valid in some of their implications.
As black holes are, at root, only theoretical concepts, this position is only to be expected, as knowledge of their real properties improves. A similar position existed with other theoretical concepts, such as "the atom". Atoms certainly exist, but graphic models of atoms have changed markedly over the years as knowledge of their properties has improved.
In this article it is implicitly assumed that Black Holes are one size-range of what are called Vortex Stars -- very rapidly spinning objects which emit beams of light, and in some cases particles, along their axes of rotation. A fuller treatment will be found in UG102: Understanding Vortex Stars -- White Dwarfs, Neutron Stars, Black Holes, and AGNs [2].
Figure F1 shows a typical current graphic representation of a Black Hole. Neutron Stars may also be represented similarly.

Figure BS809-F1. Graphic representation of a Black Hole.
The main features of the image are, a swirling, rapidly rotating disc of material, and twin beams of radiation jetting out from along the axes of the disc. The disc is essentially a vortex, and like all vortexes it tries to suck in material from outside and move it to the centre.
Quasars
The development of radio astronomy in the 1950s -- studying radiation from the Universe at wavelengths of radio, rather than light -- threw up objects which appeared to be new types of stars. These objects gained the name "Quasar".
The term quasar derives from how these objects were originally discovered [1]. Away from the plane of the Milky Way Galaxy, most radio sources were identified with otherwise normal-looking galaxies. Some radio sources, however, coincided with objects that appeared to be unusually blue stars. Because of their almost starlike appearance, they were dubbed “quasi-stellar radio sources,” which by 1964 had been shortened to “quasar.”
As more and more of these objects were discovered, they started to be grouped in different classes according their characteristics. It became clear that each quasar was the origin of light from the centre of a distant galaxy. And not only are there different types of galaxy, their appearance varies according to the direction from which they are viewed.

Figure BS809-F2. Quasar galaxy or black hole viewed from different directions.
Figure F2 shows how different names became applied to quasars according to the angle at which they were being viewed. At most angles, when they appeared of lower intensity, they became called radio galaxies or Seyfert galaxies. But when they happened to have their radiation beams aimed directly at the observer, they appeared very bright, and were called Blazars.
The centre of the disc is labelled a Black Hole. There is such an object at the heart of every galaxy. It is also called an AGN or Active Galactic Nucleus, and is classed as a Supermassive Black Hole, having millions or billions of times the mass of a star like our Sun.
Black Holes of smaller mass are formed from the blowup of ordinary (Fusion) stars, as they come to the end of their lives.
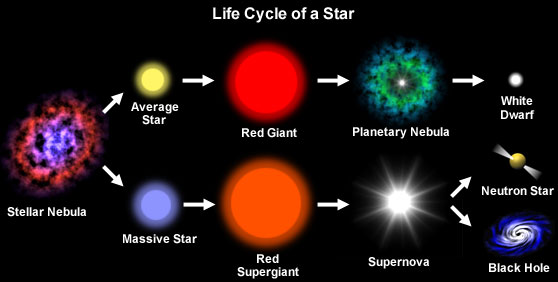
Figure BS809-F3. Life cycles of fusion stars. From [2].
All ordinary (Fusion) stars have a limited life. Surprisingly, very massive stars have quite short lives, as little as a few million years. Small-mass stars have long lives, reaching into many billions of years. All eventually reach a blowup phase, that of a Transition Star, where their outer half separates off and flies into space, leaving behind a Vortex Star.
In order of increasing mass of the remnant star left behind, this is called a White Dwarf, a Neutron Star, or a (Stellar-Mass) Black Hole, but all are Vortex Stars, differing only in mass. There is more in UG102: Understanding Vortex Stars -- White Dwarfs, Neutron Stars, Black Holes, and AGNs [2].
In addition to formation from scattered matter, all astronomical objects, from asteroids to galaxies, may increase by merger with other objects.
Figure F4 shows where various types of vortex star lie in a plot of mass against rotation rate.
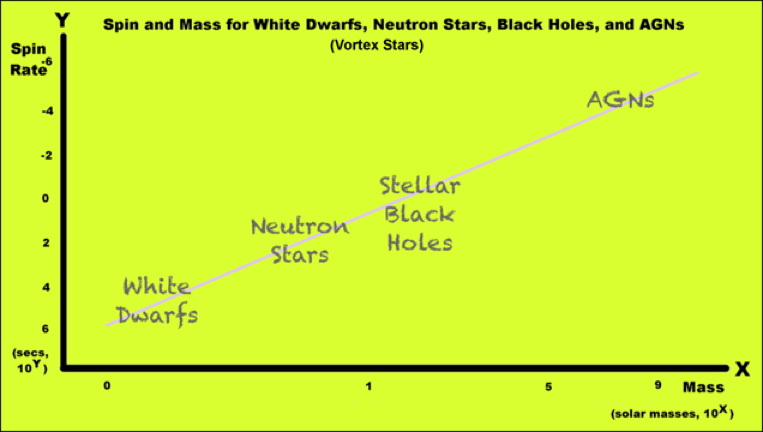
Figure BS809-F4. Mass and rotation rate in Vortex Stars.
This plot is a recent derivation. It may be a preliminary exposure of an underlying straight-line graph of mass against rotation rate. In ordinary (Fusion) stars, star mass and star lifetime are known to have a similar strong dependence.
A vital point about vortex stars, is that the light they emit is channelled into their axial beams, and not emitted in all directions like that of fusion stars. Therefore they do not follow the same laws regarding fall-off of intensity with distance of the latter.
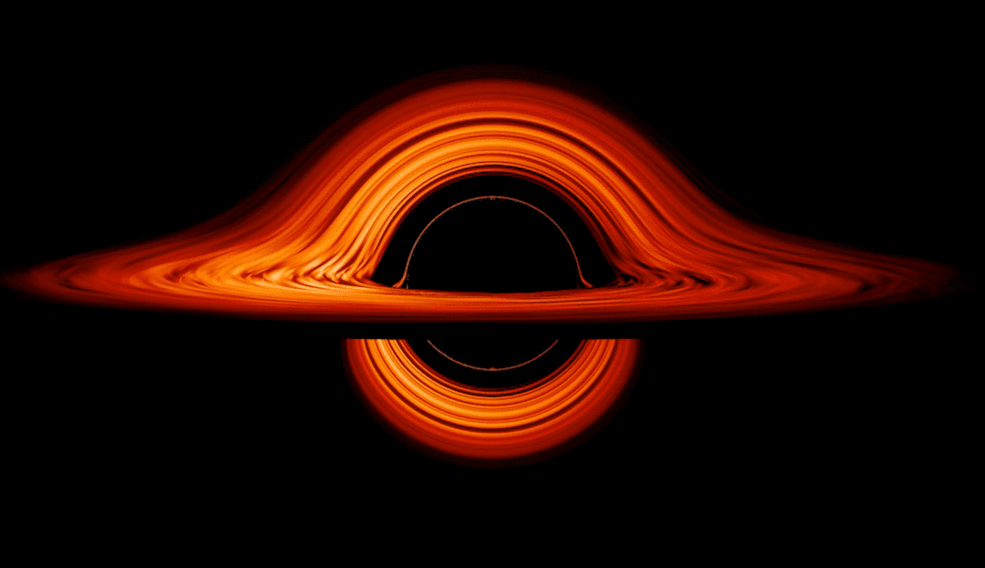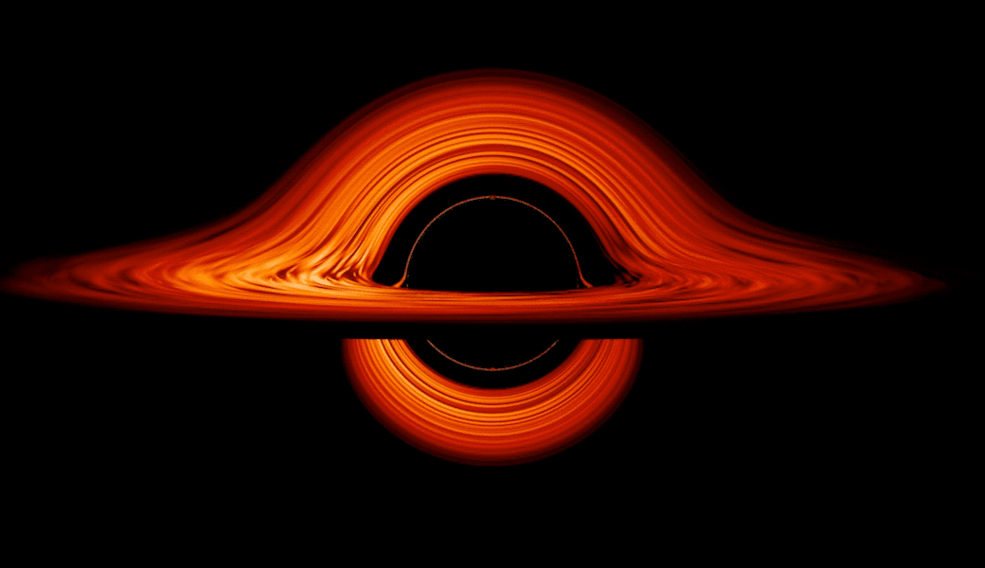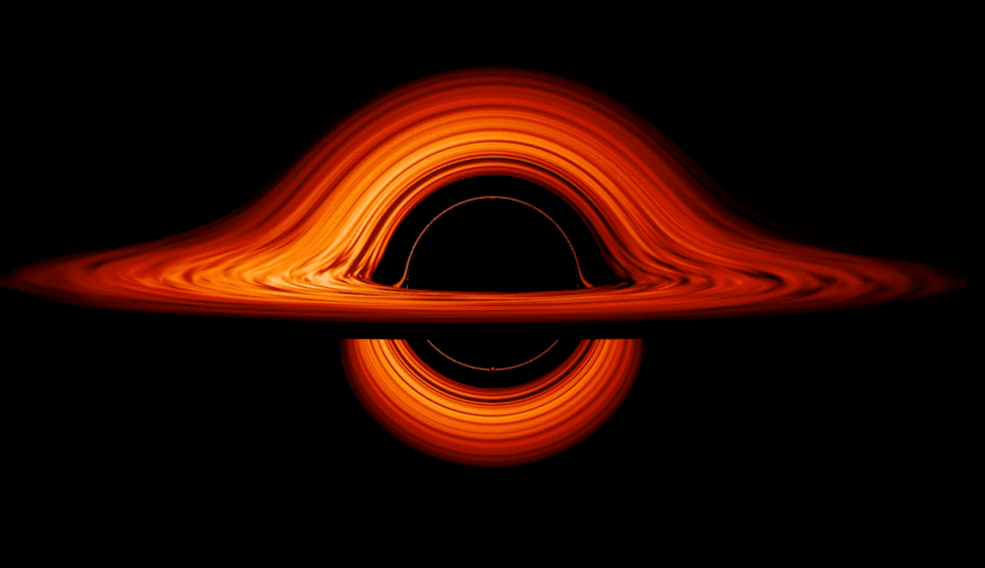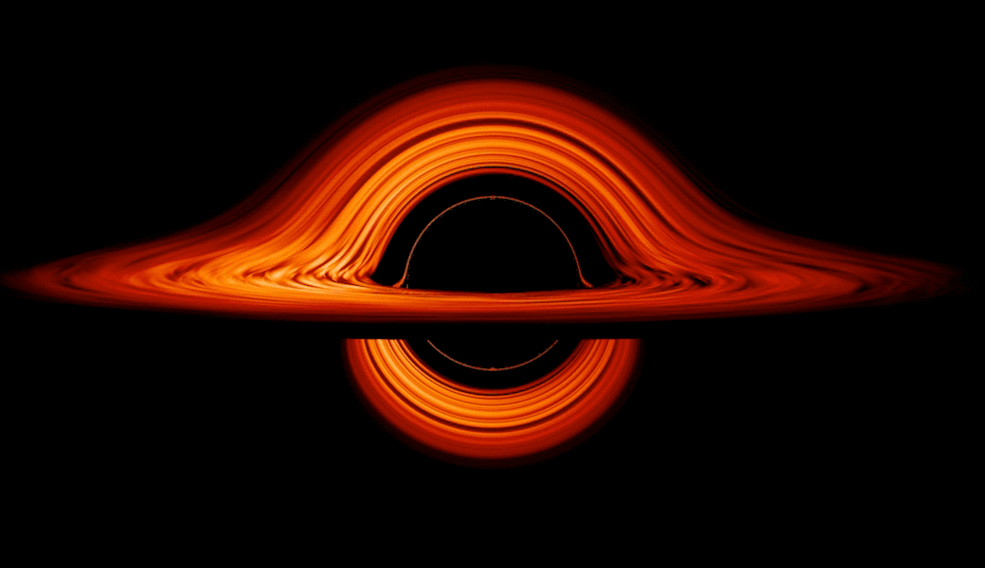
Figure BS809-F5. Swirling representation of a Black Hole.
In an effort to represent the largely uncertain, and perhaps innately weird, nature of Black Holes, another representation (Figure F5) shows one as a swirling, recycling mass, changing its form over two planes of existence.
Black Holes must be of Limited Width
A little physics shows that Black Holes must be of very limited width, unlike all the representations shown above.
The class of quasars known as Millisecond Pulsars spin very rapidly, several hundred times per second. As of 2024, the pulsar PSR J1748-2446ad, discovered in 2004, is the fastest-spinning pulsar known, spinning 716 times per second [3].
Suppose that another pulsar is found in the future, spinning slightly faster than this, at 1000 times a second (the definition of a millisecond pulsar). Suppose that it was only 100 kilometres across, less than the width of some modern cities.
The circumference of this object would be a little over 314 kilometres, and if rotating at 1000 times a second, its edge speed would be 314,000 km/sec, which exceeds the speed of light.
The surprising outcome of this calculation is that Black Holes must be quite narrow across, less than about 100 kilometres, which rules out all of the earlier representations including wide, fast-spinning discs. And a recent study [3] has been able to measure the actual width of a pulsar -- only 11.4 kilometres across.
The study [3] says: "One of the nearest pulsars, PSR J0437-4725, lies at 510 light years in the constellation Pictor. It rotates 174 times per second, which means it rotates once in just 5.75 milliseconds. Perhaps more mind blowing than its rotational velocity is its size. Imagine 1.4 times the mass of the Sun squashed up into a ball just 11.4 kilometres across -- the Sun is 1.39 million kilometres across by comparison! ".
It is already known [4] that White Dwarfs, the least massive of the Vortex Stars, decrease in size with increasing mass. In [4] it notes "White dwarfs with about half of the sun’s mass were about 1.75 times as wide as Earth. Those with slightly more mass than the sun came in closer to three-quarters the width of Earth.".
So black holes, and other vortex stars, cannot be disc-shaped. At present. we don't know about their length along their axes, or even if this dimension has any physical meaning. But a better assumption for the moment is that they are spindle-shaped.
Figure F6 is just such an animated representation of a black hole.

Figure BS809-F6. Hotrod representation of a Black Hole.
This graphic can certainly be improved by those more skilled in the graphic arts. But it does convey the essential points -- a rapidly-rotating, thin cylinder, emitting beams of radiation and particles along its two axis directions.
Some bold suggestions
It may be a diversion to consider some suggestions about how we may view the Universe. If you believe, as I do, that the Universe is infinite in space and time, you benefit from having explanations about how everything is recycled. How galaxies, stars, and planets go through their lives, and are broken up or transformed to give the substances needed to form later iterations. Essentially, active local evolution and action, and very-large-scale placidness.
Mass/Energy Recycling
We have already mentioned one of the Matter-redistribution routes, when fusion stars blow up at the end of their lives and distribute perhaps half their matter into the surrounding galaxy, and beyond. There is more detail on recycling in UG101: Recycling the Universe -- Neutron Stars, Black Holes, and the Science of Stuff [5].
When you consider Mass/Energy redistribution routes, the most prominent is the conversion of mass into energy in Fusion stars. The radiation produced from the fusion of nuclei in stars has been the focus of almost all astronomical studies up to recent times.
With increasing understanding of Vortex stars, we have a new route, which includes the production of Mass from Energy on a large scale, in the particles emitted along the beam axes of Black Holes and other Vortex Stars. Of course these beams are also prominent carriers of radiation energy.
Vortex-star beams are thus a major balancing factor in a steady-state Universe, involving conversion of energy to mass, the opposite of conversion of mass to energy in fusion stars.
We can mark this point with a Proposition.

Proposition BS809-P1.
Axial beams thus provide another source of mass which can be used to build new stars, in addition to that from fusion star blowup. Moreover, the particles involved may travel at close to the speed of light, and distribute mass far beyond their local galaxy and deep into the Universe.
Radiation in axial beams may travel huge distances -- billions of light-years -- without suffering very much attenuation. That is how we can observe vortex stars billions of light-years away. Particles in axial beams are a different matter. They will all have, or gain, charge (free neutrons will decay into charged particles), and so their paths will be altered by interstellar magnetic fields. Tracing the origin of these particles is therefore more difficult.
It's similarly difficult to measure how much of a vortex star's output is radiation, and how much is particles (mass). We might expect the proportion of particles to increase with star mass, as innate rotational energy increases, but we don't know.
It seems very probable that what we call Cosmic Rays are the combined products of these axial beams. We can put forward this as a Proposition.

Proposition BS809-P2.
Mass Gravity and Spin Gravity
Everyone is familiar with Mass Gravity, the attraction between two masses which was investigated by Isaac Newton. But Spin Gravity is much less familiar.
In brief, Spin Gravity deals with forces between bodies which are rotating. The rotation of a massive body like our Sun does exert influence on nearby bodies such as the planets, and this influence acts to make these bodies rotate in a similar way to the Sun itself. And the converse is true -- but the lighter body will show the greater effect.
There is more detail in BS806: Mass Gravity and Spin Gravity -- Adjusting the Universe [6]. Spin Gravity (one aspect of which Einstein refers to as "Frame Dragging") is a much smaller force than Mass Gravity, and so tends to show up in extreme cases (such as very long times or very large masses).
The basic law of (standard or mass) Gravity was derived by Isaac Newton back in 1687, and the usual formula quoted is as follows.
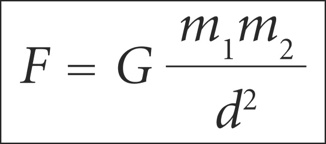 . . . (1)
. . . (1)
Figure BS809-F7. The standard Mass Gravity equation.
Following is an empirically derived equation for the gravitational forces due to spin gravity, a consequence of the rotation of the bodies involved [6].
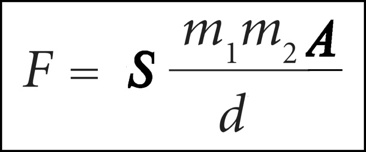 . . . (2)
. . . (2)
Figure BS809-F8. The Spin Gravity equation.
There are two major differences in the impact of these two equations. The first is that in Mass Gravity, the force falls away with the inverse of d2 (distance squared), while with Spin Gravity the force falls away directly with inverse distance (d). The effect is that Mass Gravity tends to predominate at shorter distance, while Spin Gravity, even if weaker, can come to predominate at bigger distances.
This difference provides an alternative explanation for a phenomenon usually attributed to Dark Matter. This concerns the rotation curves of distant galaxies.
Rotation Curves of Galaxies"The rotation curve of a disc galaxy is a plot of the orbital speeds of visible stars or gas in that galaxy versus their radial distance from that galaxy's centre. It is typically rendered graphically as a plot. A significant discrepancy exists between the experimental curves observed, and a curve derived by applying gravity theory to the matter observed in a galaxy. Theories involving dark matter are the main postulated solutions to account for the variance."
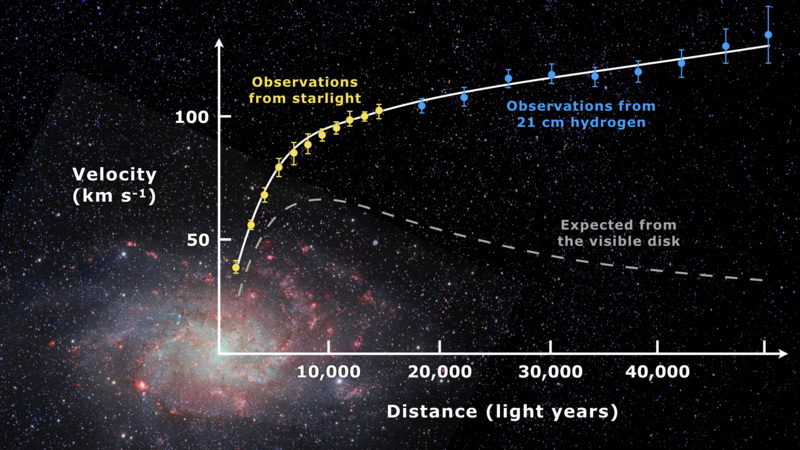
Figure BS809-F9. Rotation curve of spiral galaxy Messier 33. From [7].
So, the existence of a Dark Matter halo around a galaxy is currently a common explanation of the shape of these curves. At present a simple mathematical treatment of this concept is not readily available.
Other explanations for the rotation curves have been put forward, such as modifications to Newton's gravity laws. It seems to me that the influence of Spin Gravity on the situation provides a better answer.

Proposition BS809-P3.
Look again at the rotation curve shown in Figure F8. The initial part, shown in yellow dots, is a smooth curve, reflecting where Mass Gravity predominates. In this section, the curve fits with the idea of falling away with d2, distance squared.
The blue dots then correspond with where Spin Gravity takes over. Although intrinsically weaker than Mass Gravity, Spin Gravity only falls with d, simple distance, and thus gives a straight line.
Incidentally, this reasoning does give a way of inter-relating the two types of gravity equation shown above, as the factor "d" is the same in both equations. So the value of d where the curve changes to a straight line will be where the two types of gravity are equal.
The second way in which the gravity equations differ is in the inclusion of the parameter "A" on the right-hand side. A is a vector quantity, defining the angle between the axes of rotation of the two bodies concerned (if their axes are collinear, A equals 0). For those interested in dimensional analysis, A has dimensions of 1/L.
The "m" values in the Spin Gravity equation are also the same as for Mass Gravity. But there is a twist -- they are the values of the rotational energies of the two bodies, but energies treated as masses.
Equivalence of Mass and Energy
The famous Einstein equation E=mc2 tells us how energy and mass are related. It's usually read as "energy equals mass times the speed of light squared". This is correct. However the usual interpretation of this is that mass can be converted into energy, or energy converted into mass, and the formula can be used to calculate the sizes of the initial and final products.
In the present instance, a different aspect of the position can be had by saying that energies and masses are just different views of the same situation, and the equation just allows to put numbers on the different approaches. This is useful when we need to consider the enormous rotational energies of vortex stars.

Proposition BS809-P4.
In the Einstein equation, energy means energy, and this includes rotational energy. In everyday life, rotational energy does not often figure very large, except in a few cases like the physics of flywheels. But in vortex stars, rotation holds some of the largest quantities known.
As of 2024, the most massive AGN yet discovered [8] is the supermassive black hole at the centre of the galaxy known as Abell 1201. This has a mass of 33 billion times that of our Sun. It was discovered using gravitational lensing.
So the AGN known as Abell 1201 is the most massive single object known in our Universe. Is there an upper limit to such masses? Let's look at a little more theory.
Look again at Figure F4, the plot of mass against spin rate for vortex stars.

Figure BS809-F4/2. Mass and rotation rate in Vortex Stars.
It was suggested earlier than this plot could be a first stab at an underlying linear relationship. If Proposition P4 holds, you can see that this must be so -- essentially the plot is of mass against mass, mass against itself. This must be a straight line.
A good mathematician should be able to check this, using examples of vortex stars for which both spin rate and mass are both accurately known. There are complications -- the rotational energy of a spinning black hole will depend on how its mass is distributed, and whether all parts rotate at the same rate. This is currently unknown.
How do Vortex Stars get so massive?
An interesting facet of the physics of rotating bodies is that, for a given conformation, rotational energy increases as the square of the spin rate, so doubling the rotation rate of a solid cylinder will increase its spin energy by four times. Halving the diameter of a rotating cylinder will lead to a similar increase. Rotational energy may also be called angular momentum.
If energy is the same as mass, then the vortex action of a star or galaxy in drawing in objects orbiting its remote reaches will increase its mass in two ways. First, the mass of the planet or solar system swallowed will be added to that of the central body. Second, the rotational energies of the added object, both from its own rotation and its orbital energy, will be added to the central body.
Rotational energy, like other forms of energy, is conserved. Suppose you moved the Earth inward to sit on the Sun's equator, where it might well break up and scatter. The Sun would gain the Earth's mass, and also its orbital energy. As the initial Earth orbit is about 150 million km from the Sun's centre, and its surface is only about 0.7 million km from its centre, the additional rotational energy would be very significant.
Conservation of rotational energies in the Universe also explains a number of other phenomena, such as why a fusion star transitions to a vortex star at the end of its life. It may also explain why vortex stars may have an upper mass limit, and how they generate their axial beams.
How Vortex Stars generate their axial beams
While the fact that fast-spinning black holes emit axial beams of light and particles is now generally accepted, how they do this has until now been largely speculative.
Here is part of an explanation, from [9]. "At the centers of some galaxies are supermassive black holes that can hold more material than a billion Suns, theorists say. From some of these galaxies, focused beams of hot gas shoot into space at more than 99 percent the speed of light. The plasma emits X-rays, radio waves and other radiation, all of which has been widely observed. The black hole is spinning very fast, and according to Einstein it drags space-time with it. "
As mentioned above, "frame-dragging", or the dragging of part of the space-time continuum, is predicted in Einstein's General Relativity, an aspect here called Spin Gravity.
However most current explanations include ideas of wide "accretion discs" spinning around black holes, and we have seen that these cannot exist. A good understanding of how axial beams must be generated in vortex stars comes from the fact that matter cannot travel faster than the speed of light.

Proposition BS809-P5.
This model, that of ever-increasing Vortex Star rotational energy approaching the light-speed limit and forcing shedding though the axial beams, does give some answers to currently uncertain questions. We can view a galaxy as a rapidly-spinning vortex slowly drawing in objects to its centre.
Every extra object it swallows will be reflected in the axial-beam output. Adding a small planet might lead to a Fast Radio Burst output, sucking in a star might give a higher-energy outcome, in visible light, ultraviolet, or x-ray ranges.
These are one-off events in vortex-star outputs. Regular events, as with pulsars, may just be because companion bodies or other effects cause repeated slight deviations in beam directions.
If this model is valid (that is, it gives a good match with what is observed), then it might mean that a true millisecond pulsar, spinning at 1000 times a second, may not be possible. Currently-known real cases, with masses of 33 billion Suns, or rotations of 716 times a second, may be near the limit.
We can call this ceiling to vortex star mass or energy the "Millisecond Limit". Because rotational energy increases as the square of rotation speed, a Millisecond Object would actually have almost twice the mass or energy of one rotating 716 times a second.
What happens when combining objects exceed the Millisecond Limit? Adding a lot more mass or rotational energy, as with two black holes merging, may force a sudden rapid release of radiation and particles, to keep the combined product below the limit.
Here, then, is an explanation for what are called Gamma-Ray Bursts. In [10] it was announced that a recently detected cosmic gamma-ray burst was as bright as the "rest of the universe" put together, releasing a hundred times more energy than previously theorized.

Proposition BS809-P6.
The team in [10] measured the distance to a faint galaxy from which the burst, designated GRB 971214, originated. It is about 12 billion light years from the Earth. The burst appears to have released several hundred times more energy than an exploding star, called a supernova, until now the most energetic phenomenon in the universe known to scientists. The article commented "The origin of the bursts remains a mystery".
It appears that the role of rotational energy in celestial objects, and in particular its conservation, deserves more attention in understanding the Universe. Another area where this may be pertinent is in the transition of a Fusion star into a Vortex star. This merits a separate article.
* * * * * * * * * * * * * * * * * *

References and Links
[1]. Quasar . https://www.britannica.com/science/quasar .
[2]. David Noel. UG102: Understanding Vortex Stars -- White Dwarfs, Neutron Stars, Black Holes, and AGNs . http://aoi.com.au/UG/UG102/index.htm .
[3]. Mark Thomson. A Close Pulsar Measures 11.4 km Across. Universe Today, July 13, 2024. https://www.universetoday.com/167753/a-close-pulsar-measures-11-4-km-across/ .
[4]. Maria Temming. Strange but true: White dwarfs shrink as they gain mass. https://www.snexplores.org/article/white-dwarfs-shrink-as-they-gain-mass .
[5]. David Noel. UG101: Recycling the Universe -- Neutron Stars, Black Holes, and the Science of Stuff. http://www.aoi.com.au/Recycling .
[6]. David Noel. BS806: Mass Gravity and Spin Gravity -- Adjusting the Universe. http://www.aoi.com.au/BaseScience/BS806/index.htm .
[7]. Galaxy rotation curve. https://en.wikipedia.org/wiki/Galaxy_rotation_curve .
[8]. James Nightingale. Discovering the biggest known black hole in Abell 1201. https://www.skyatnightmagazine.com/space-science/ultramassive-black-hole-abell-1201 .
[9]. Robert Roy Britt. Twisted Physics: How Black Holes Spout Off. https://www.space.com/261-twisted-physics-black-holes-spout.html .
[10]. Gamma-ray Burst Most Energetic Event in the Universe!
. https://en.wikipedia.org/wiki/Millisecond_pulsar .
Go to the Base Sciences Home Page

Version 1.0 compilation started 2023 Dec 13. First version 1.0 on Web 2024 Jul 31.










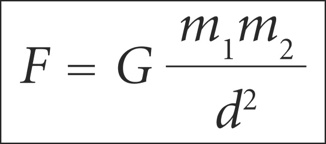 . . . (1)
. . . (1)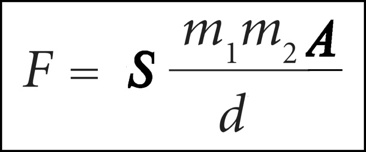 . . . (2)
. . . (2)






